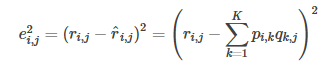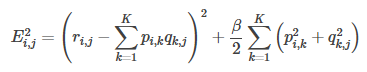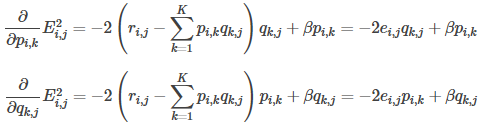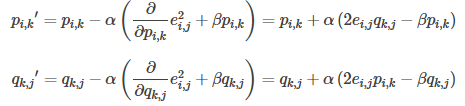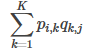1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| from numpy import *
def load_data(path):
f = open(path)
data = []
for line in f.readlines():
arr = []
lines = line.strip().split("\t")
for x in lines:
if x != "-":
arr.append(float(x))
else:
arr.append(float(0))
#print arr
data.append(arr)
#print data
return data
def gradAscent(data, K):
dataMat = mat(data)
print (dataMat)
m, n = shape(dataMat)
p = mat(random.random((m, K)))
q = mat(random.random((K, n)))
alpha = 0.0002
beta = 0.02
maxCycles = 10000
for step in range(maxCycles):
for i in range(m):
for j in range(n):
if dataMat[i,j] > 0:
#print dataMat[i,j]
error = dataMat[i,j]
for k in range(K):
error = error - p[i,k]*q[k,j]
for k in range(K):
p[i,k] = p[i,k] + alpha * (2 * error * q[k,j] - beta * p[i,k])
q[k,j] = q[k,j] + alpha * (2 * error * p[i,k] - beta * q[k,j])
loss = 0.0
for i in range(m):
for j in range(n):
if dataMat[i,j] > 0:
error = 0.0
for k in range(K):
error = error + p[i,k]*q[k,j]
loss = (dataMat[i,j] - error) * (dataMat[i,j] - error)
for k in range(K):
loss = loss + beta * (p[i,k] * p[i,k] + q[k,j] * q[k,j]) / 2
if loss < 0.001:
break
#print step
if step % 1000 == 0:
print (loss)
return p, q
if __name__ == "__main__":
dataMatrix = load_data("F:/input.txt")
p, q = gradAscent(dataMatrix, 5)
'''
p = mat(ones((4,10)))
print p
q = mat(ones((10,5)))
'''
result = p * q
#print p
#print q
print (result)
|