前缀树与后缀树
1.前缀树
1.1 概述
前缀树又名字典树,单词查找树,Trie树,是一种多路树形结构,是哈希树的变种,和hash效率有一拼,是一种用于快速检索的多叉树结构。
典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
Trie树也有它的缺点,Trie树的内存消耗非常大。
性质:不同字符串的相同前缀只保存一份。
操作:查找,插入,删除。
举个栗子:给出一组单词,inn, int, at, age, adv,ant, 我们可以得到下面的Trie: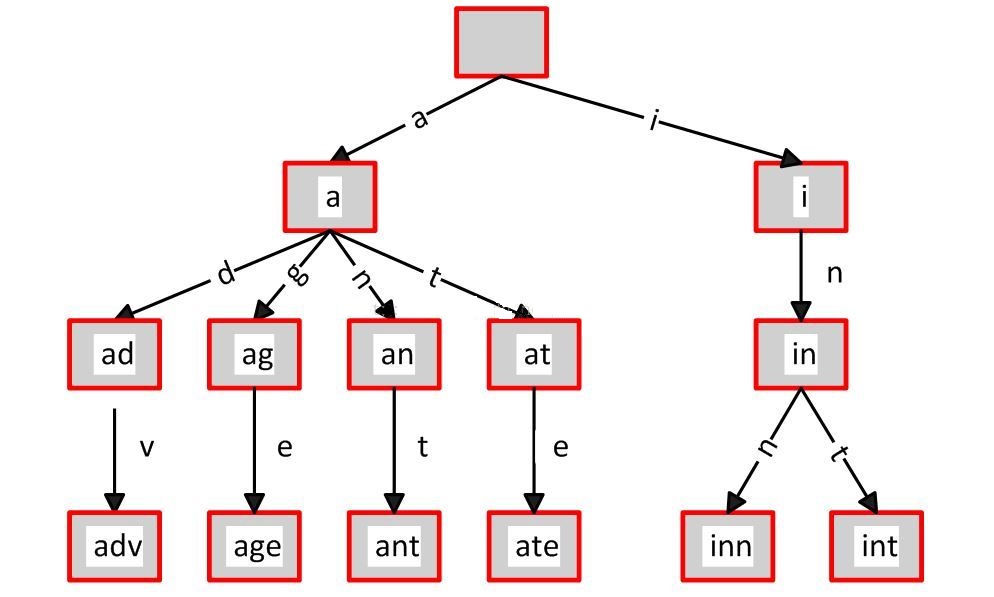
从上面可以发现一些Trie树的特性:
1)根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
2)从根节点到某一节点的路径上的字符连接起来,就是该节点对应的字符串。
3)每个节点的所有子节点包含的字符都不相同。
4)每条边对应一个字母。每个节点对应一项前缀。叶节点对应最长前缀,即单词本身。
单词inn与单词int有共同的前缀“in”, 因此他们共享左边的一条分支,root->i->in。同理,ate, age, adv, 和ant共享前缀”a”,所以他们共享从根节点到节点”a”的边。
查询操纵非常简单。比如要查找int,顺着路径i -> in -> int就找到了。
搭建Trie的基本算法也很简单,无非是逐一把每则单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在,就共享,否则创建对应的节点和边。比如要插入单词add,就有下面几步:
考察前缀”a”,发现边a已经存在。于是顺着边a走到节点a。
考察剩下的字符串”dd”的前缀”d”,发现从节点a出发,已经有边d存在。于是顺着边d走到节点ad
考察最后一个字符”d”,这下从节点ad出发没有边d了,于是创建节点ad的子节点add,并把边ad->add标记为d。
1.2 应用
前缀树还是很好理解,它的应用也是非常广的。
(1)字符串的快速检索
字典树的查询时间复杂度是O(logL),L是字符串的长度。所以效率还是比较高的。字典树的效率比hash表高。
hash表:
通过hash函数把所有的单词分别hash成key值,查询的时候直接通过hash函数即可,都知道hash表的效率是非常高的为O(1),当然这是对于如果我们hash函数选取的好,计算量少,且冲突少,那单词查询速度肯定是非常快的。那如果hash函数的计算量相对大呢,且冲突律高呢?这些都是要考虑的因素。
还有就是hash表不支持动态查询,什么叫动态查询,当我们要查询单词apple时,hash表必须等待用户把单词apple输入完毕才能hash查询。当你输入到appl时肯定不可能hash吧。
字典树(tries树):
对于单词查询这种,还是用字典树比较好,但也是有前提的,空间大小允许,字典树的空间相比较hash还是比较浪费的,毕竟hash可以用bit数组。
(2)字符串排序
从上图我们很容易看出单词是排序的,先遍历字母序在前面。
减少了没必要的公共子串。
(3)最长公共前缀
inn和int的最长公共前缀是in,遍历字典树到字母n时,此时这些单词的公共前缀是in。
(4)自动匹配前缀显示后缀
我们使用辞典或者是搜索引擎的时候,输入appl,后面会自动显示一堆前缀是appl的东东吧。
那么有可能是通过字典树实现的,前面也说了字典树可以找到公共前缀,我们只需要把剩余的后缀遍历显示出来即可。
2.后缀树
2.1概述
后缀树,就是把一串字符的所有后缀保存并且压缩的字典树。相对于字典树来说,后缀树并不是针对大量字符串的,而是针对一个或几个字符串来解决问题。比如字符串的回文子串,两个字符串的最长公共子串等等。
性质:一个字符串构造了一棵树,树中保存了该字符串所有的后缀。
操作:就是建立和应用。
(1)建立后缀树
比如单词banana,它的所有后缀显示到下面的。0代表从第一个字符为起点,终点不用说都是字符串的末尾。
以上面的后缀,我们建立一颗后缀树。如下图,为了方便看到后缀,我没有合并相同的前缀。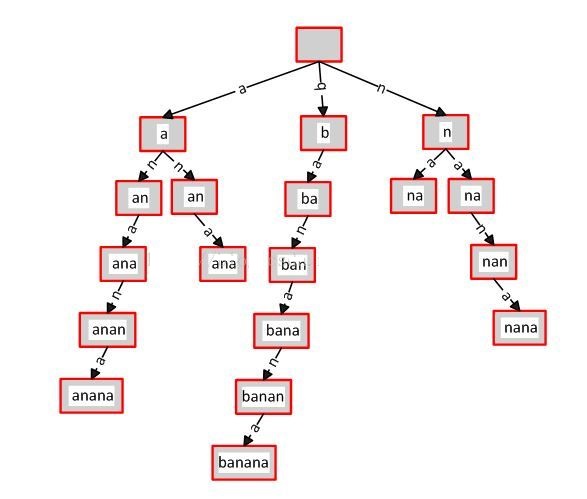
前面简介的时候我们说了,后缀树是把一个字符串所有后缀压缩并保存的字典树。所以我们把字符串的所有后缀还是按照字典树的规则建立,就成了下图的样子。这就是后缀树的压缩,可见更加节省空间。
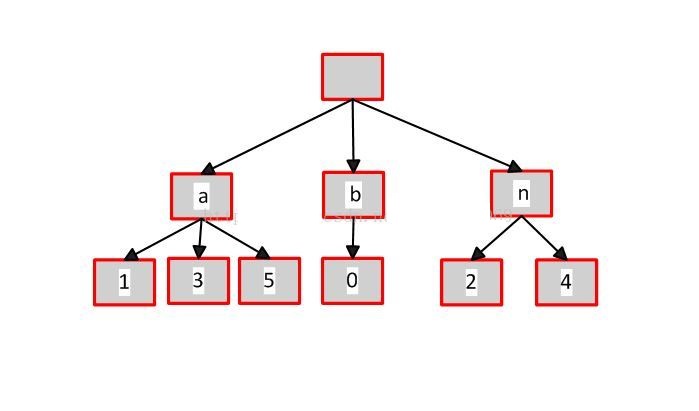

注意还是和字典树一样,根节点必须为空。
2.2应用
后缀树能解决大多数字符串的问题
(1)查找某个字符串s1是否在另外一个字符串s2中
这个很简单,如果s1在字符串s2中,那么s1必定是s2中某个后缀串的前缀。
理解以下后缀串的前缀这个词,其实每个后缀串也就是起始地点不同而已,前缀也就是从开头开始结尾不定。
后缀串的前缀就可以组合成该原先字符串的任意子串了。
比如banana,anan是anana这个后缀串的前缀。
(2)指定字符串s1在字符串s2中重复的次数
比如说banana是s1,an是s2,那么计算an出现的次数实际上就是看an是几个后缀串的前缀。
上图的a节点是保存所有起始为a字母的后缀串,我们看a字母后的n字母的引用计数即可。
(3)两个字符串S1,S2的最长公共部分(广义后缀树)
(4)最长回文串(广义后缀树)

